Lastnosti dokumenta
- Naslov
- Celularni programski algoritem
- Del
- Polnjenje pravokotnika
- Datum vsebine
- 31. 05. 2007
- Original
- cpa_rectbound.pdf
- Vrsta
- seminarska naloga
- Jezik
- slovenščina
- Različica
- 1.0
- Ustanova
- Fakulteta za računalništvo in informatiko, Univerza v Ljubljani
- Študij
- Računalništvo in informatika, Logika in sistemi, 4. letnik
- Predmet
- Celularne strukture in sistemi
- Mentor
- dr. Branko Šter
- Avtor
- Tine Lesjak
- Ocena
- 10 od 5-10
Priloge
- cpa_rectbound.zip
- Implementacija algoritma v Javi 1.4.2, skupaj z izvorno kodo in dokumentacijo (javadoc).
Osnovni parametri se nastavijo v kodi - ni vhodnih parametrov. - cpalg.pdf
- CPA po Mosheju Sipperju
Opis problema
Cilj naloge je s pomočjo celularnega programskega algoritma (CPA) razviti nabor pravil, ki v celularnem avtomatu (CA) napolnijo prostor pravokotne oblike omejen s štirimi stranicami - pravokotnik. Pri tem ostane prostor zunaj pravokotnika prazen.
Algoritem je razvit iz CPA-ja dr. Mosheja Sipperja. Njegov opis algoritma in knjigo Evolution of Parallel Cellular Machines je moč dobiti na spletni strani http://www.moshesipper.com/.
Specifikacije
Lastnosti celularnega avtomata (prostora) in algoritma:
- CA je dvodimenzionalen.
- CA je 2-stanjski. Stanje celice je lahko 1 (true) ali 0 (false).
- CA je neuniformen. Vsaka celica ima svoje pravilo.
- Sosednost je 5 (von Neumannova sosednost). Sosedne celice so poleg sebe zgoraj, desno, spodaj in levo.
- Začetna pravila so naključna.
- Vsak pravokotnik (ne cel CA) je napolnjen z enicami in ničlami naključno tako, da je zagotovljena večja variabilnost: najprej se naključno določi razmerje enic in ničel, nato se glede na razmerje naključno določijo stanja celic.
- Pravila so 32 bitna (25).
- CA ni cikličen. Celice, ki padejo izven prostora, imajo stanje 0. Fitnes celic izven prostora je 0. Pravila izven prostora imajo kodo 0.
- Stranice oz. robovi pravokotnika so ob vsaki začetni konfiguraciji nastavljeni naključno tako, da ne dosežejo roba prostora in da ne presežejo polovice prostora. Na primeru CA velikosti 8 x 8 celic (1-8):
- zgornji in levi rob: 2, 3 ali 4,
- spodnji in desni rob: 5, 6 ali 7.
- Spremembe stanj sosednjih celic so opisane po bitih pravila po vrsti: sredinska (ta), zgornja, desna, spodnja in leva.
Nastavljive lastnosti, na katerih sem izvajal meritve:
- CA je velik 8 x 8 celic. Ima 64 celic.
- Število izvajanj posamezne začetne konfiguracije (M) je 12.
- Število začetnih konfiguracij (C) je 200.
- Število generacij (G) je odvisno od meritve. Uporabil sem vrednosti 500 in 5000.
- Verjetnost mutacije pravila pri evoluciji je 0,001. Mutacija se zgodi le, če sta več kot dve sosednji pravili boljši (imata večji fitnes).
- Pri zadnji meritvi sem ob začetni konfiguraciji dodatno nastavil stanja celic v vseh štirih kotih pravokotnika na 1.
Algoritem sem napisal v programskem jeziku Java (različice 1.4.2). Razvijal sem ga v razvojnem okolju Eclipse.
Meritve
Meritve sem opravljal na svojem delovnem računalniku, ki ima 1500 MHz procesor AMD in 1 GB pomnilnika.
Meritve sem opravil na treh različnih konfiguracijah algoritma. Pri 1. sem pognal 500 generacij, pri 2. pa 5000. Pri 3. konfiguraciji sem po naključni napolnitvi pravokotnika dodatno nastavil stanja celic v njegovih kotih na 1 ter pognal algoritem za 5000 generacij.
Vsako konfiguracijo algoritma sem pognal petkrat in za prikaz meritev izbral eno, na oko najprimernejšo.
| Konfiguracija algoritma | Uspešnost nabora pravil | Najuspešnejša generacija | Število izvedenih generacij | Trajanje izvajanja |
|---|---|---|---|---|
| 1. | 88,34 % | 341. | 500 | 14,77 s |
| 2. | 91,07 % | 4367. | 5000 | 143,41 s |
| 3. | 100,00 % | 1578. | 1578 | 46,34 s |
Tabela 1 - Rezultati meritev.
Uspešnost pravil
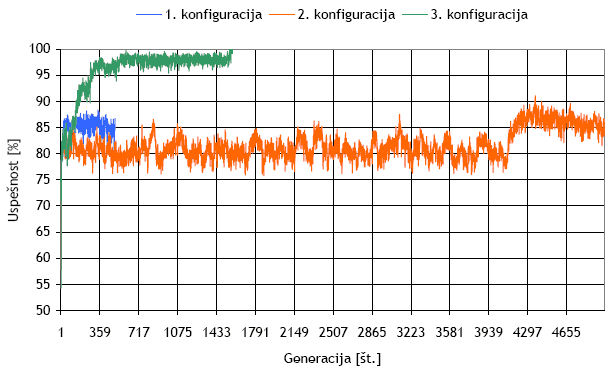
Graf 1 - Časovni potek (po generacijah) povprečne uspešnosti nabora pravil za vse tri konfiguracije algoritma. Graf prikazuje uspešnost od 50 % navzgor.
Razvoj pri najboljših pravilih
V spodnjih tabelah so zapisana stanja posameznih celic CA-ja ob začetni (naključni) konfiguraciji (0) in razvoj vseh dvanajstih korakov (1-12) ob najboljšem naboru pravil, ki je nastopil v najboljši generaciji. S sivo barvo je označen prostor zunaj pravokotnika (črne celice so znotraj pravokotnika).
00000000
00000000
01111100
01010010
00110100
00000000
00000000
00000000
(0)
00000000
00100000
00111100
00011000
01111010
00000000
00000000
00000000
(1)
00000000
01010000
00111100
00111110
01111100
00000010
00000000
00000000
(2)
00000000
01010000
01011100
00111110
01111100
00000110
00000000
00000000
(3)
00000000
00010000
00111100
01011110
01111100
00000100
00000000
00000000
(4)
00000000
00010000
00111100
01011110
01111110
00000000
00000000
00000000
(5)
00000000
00010000
00111100
01011110
01111110
00000010
00000000
00000000
(6)
00000000
00010000
00111100
01011110
01111110
00000110
00000000
00000000
(7-12)
Tabela 2 - Časovni razvoj začetne konfiguracije CA-ja pri najboljšem naboru pravil pri 1. konfiguraciji algoritma. Od koraka 7 dalje CA ostane enak. Pravilnost CA-ja je 90,63 %.
00000000
00000000
00111100
00011100
00110100
00110100
00000000
00000000
(0)
00000000
00000000
00111100
00111100
00110100
00111100
00000100
00000000
(1)
00000000
00000000
00111100
00111100
00111100
00111100
00001000
00000000
(2-12)
Tabela 3 - Časovni razvoj začetne konfiguracije CA-ja pri najboljšem naboru pravil pri 2. konfiguraciji algoritma. Od 2. koraka dalje ostane CA enak. Pravilnost CA-ja je kar 98,44 % - samo ena celica ima napačno stanje.
00000000
00000000
00110110
00011110
00110110
00000000
00000000
00000000
(0)
00000000
00000000
00111110
00111110
00111110
00000000
00000000
00000000
(1-12)
Tabela 4 - Časovni razvoj začetne konfiguracije CA-ja pri najboljšem naboru pravil pri 3. konfiguraciji algoritma. Že v 1. koraku CA doseže 100 % pravilnost.
Najpogostejša pravila
Pravila so zaradi svoje velikosti (32 bitna) zapisana v šestnajstiški obliki s pripono "0x".
| Pravilnostna tabela | 0xFFFFAFF0 |
0xFFFFDE68 |
0x80998408 |
|---|---|---|---|
0000000001000100001100100001010011000111010000100101010010110110001101011100111110000100011001010011101001010110110101111100011001110101101111100111011111011111 |
00001111111101011111111111111111 |
00010110011110111111111111111111 |
00010000001000011001100100000001 |
Tabela 5 - Tri najpogostejša pravila v vseh treh konfiguracijah algoritma.
Seznam ostalih zelo pogostih pravil:
0x7F78AAC0
0xE4BE70A2
0x2E75604C
0xFFFFEEEC
0xFFFE97B4
0xFFFFEFF0
Sklep
Meritve so pokazale razmeroma slab rezultat. Uspešnost pravil bi se naj gibala med 90 % pa vse tja do 99 %. Vse to nakazuje, da bi bilo treba algoritem izvajati dlje časa, na precej večjem številu generacij (10-100 krat).
Zanimivo pa je, da je v 3. konfiguraciji algoritma, kjer sem stanja celic v kotih pravokotnika nastavil na 1, uspešnost precej večja. Večkrat (v mojem primeru kar trikrat od petih poskusov) je uspešnost tudi 100 % in to na primeru "samo" 5000 generacij.
Najpogostejša pravila so bolj ali manj enaka. V bistvu popolnoma enakih pravil niti ni tako veliko, saj se večinoma razlikujejo le v enem, morda dveh bitih. V sredini pravokotnika so tako v večini pravila, ki se pričnejo z 0xFFFF.
 §
§